PSense

Tutorial 3: Unknown Vending Machine

Build Models in PSI

The following program models the behavior of an unknown vending machine with two buttons a and b selling only bagels and cookies. We do not know which button is for bagels, but we observe Sally, who wants a cookie, presses button b. Suppose Sally knows the how the machine works, how can we infer the probability that b gives bagels from Sally’s action?

a := 0;
b := 1;
actionPrior := [0.5, 0.5];
def vendingMachine(action: R, aEffects: R[], bEffects: R[]){
        if(action == a) {return categorical(aEffects);}
        else if(action == b){return categorical(bEffects);}
        else{return 2;}
}
def chooseAction(goal: R, aEffects: R[], bEffects: R[]){
        action := categorical(actionPrior);
        observe(goal == vendingMachine(action, aEffects, bEffects));
        return action;
}
def main(){
        aEffects := [beta(1,1), 0];
        bEffects := [beta(1,1), 0];
        aEffects[1] = 1-aEffects[0];
        bEffects[1] = 1-bEffects[0];
        goal := flip(0.5);
        observe(goal == 1 && sample(Marginal(chooseAction(goal, aEffects, bEffects)== b)));
        return bEffects[0];
}

Here is what the program does:

• In the main function, we set the prior distributions for two buttons’s effects and Sally’s goal:

        aEffects := [beta(1,1), 0];
        bEffects := [beta(1,1), 0];
        aEffects[1] = 1-aEffects[0];
        bEffects[1] = 1-bEffects[0];
        goal := flip(0.5);
  

  We don’t know how button a and b works, so we suppose the probability that they give bagels follows a Beta distribution with two parameters $\alpha=1$ and $\beta=1$. beta(1,1) samples the probability that a gives bagel and is stored in aEffects[0]; the probability that a gives cookie would be 1-aEffects[0] and is stored in aEffects[1]. The same is for b. We suppose Sally’s goal follows a Bernoulli distribution with 0.5 probability to be bagel (encoded as 0) or cookie (encoded as 1).

• If a is pressed, whether the vending machine gives bagel or cookie follows the probabilities stored in aEffects. We use categorical(aEffects) to sample bagel or cookie and return the result as what the vending machine releases. The result is encoded as 0 for bagel and 1 for cookie. The same is for b. If other buttons are pressed, return nothing (encoded as 2).

  def vendingMachine(action: R, aEffects: R[], bEffects: R[]){
        if(action == a) {return categorical(aEffects);}
        else if(action == b){return categorical(bEffects);}
        else{return 2;}
  }
  

• When Sally decides her action, she anticipates her action would allow the vending machine to release something that fulfills her goal. We can suppose Sally’s action follows some prior distribution actionPrior and use observe to condition the fact that what the machine returns meets her goal.

  def chooseAction(goal: R, aEffects: R[], bEffects: R[]){
        action := categorical(actionPrior);
        observe(goal == vendingMachine(action, aEffects, bEffects));
        return action;
  }
  

• Sally’s behavior follows the distribution given by chooseAction(goal, aEffects, bEffects) == b). We can model her pressing b by sampling from her behavior function chooseAction. The function Marginal around chooseAction gives the marginal distribution of Sally’s behavior. The function sample samples from this distribution. We observe the sampled result is equal to b. Also, we know Sally’s goal is to get a cookie (1). Combining our knowledge about Sally together, we have:

  observe(goal == 1 && sample(Marginal(chooseAction(goal, aEffects, bEffects) == b)));
  

• Given these knowledge about Sally, we want to know what is the posterior distribution of pressing b giving bagel, so we return bEffects[0] in the main function.

• The result given by PSI in Wolfram Language is:

  p[r1_] := -6/7*Boole[-1+r1<=0]*Boole[-r1<=0]*r1+10/7*Boole[-1+r1<=0]*Boole[-r1<=0]
  

  which is the probability density function of the posterior of bEffects[0]. r1 represents the value of bEffects[0].

The code snippet can be found here. This model is modified from one example in Probabilistic Models of Cognition (2nd Edition) Chapter 06.

Find Sensitivity with PSense

Notice that we suppose the probability that pressing the button giving bagels follows the distribution is given by beta(1,1). There are two constant parameters 1 in the Beta distribution, changing which would give us different results. We want to analyze the sensitivity of this program if we change the parameters of the prior. Specifically, we model the change with ?eps. For example, we can change the first parameter of aEffects[0]’s prior by:

        aEffects := [beta(1+?eps,1), 0];
        ...

The change in the prior distribution (when ?eps = 0.1) is shown in the following figure. We want to know how does this change affects the output distribution.

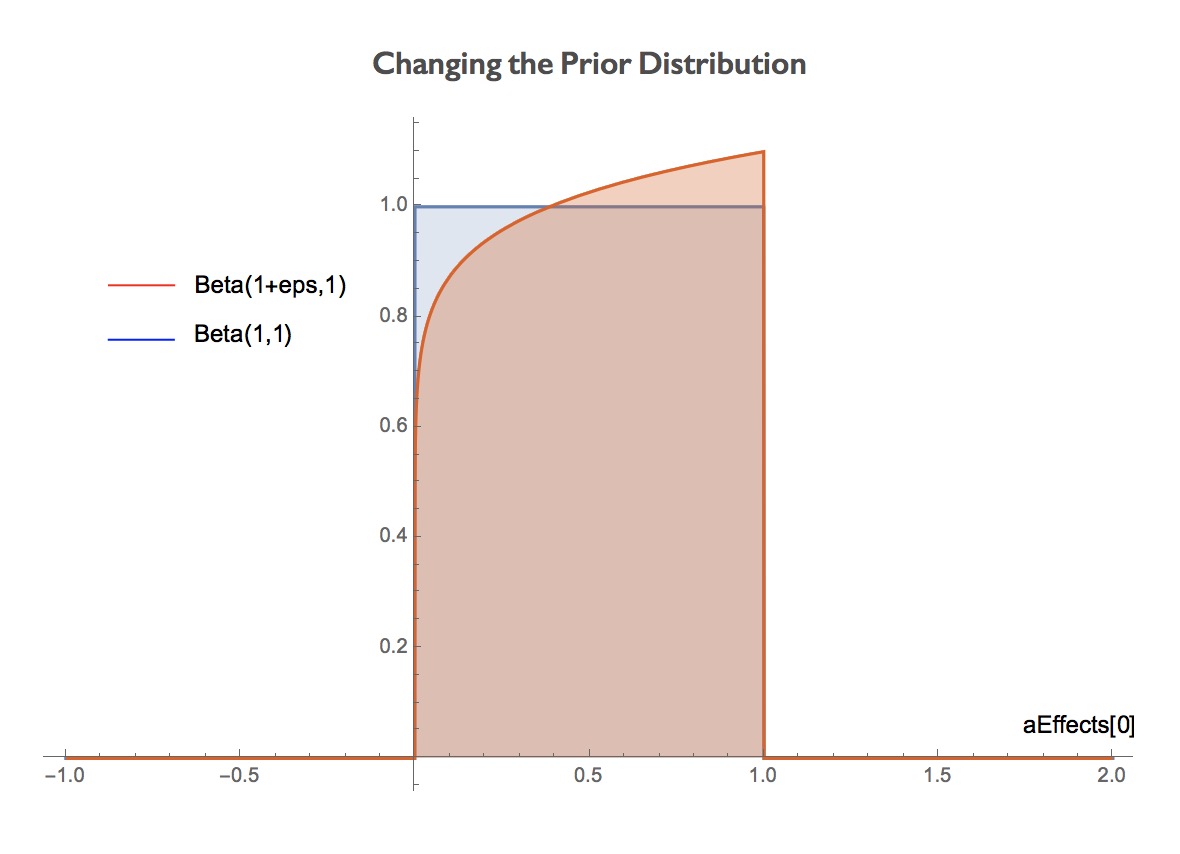
PSense can automatically add ?eps to each constant parameters and find the sensitivity of the probabilistic program. Run the following in shell prompt:

psense -f examples/unknown_vending_machine.psi

After changing the first parameter, PSense outputs:

Function Type:
Continuous
┌Analyzed parameter 1────────
│ ...

Then PSense gives the results for different metrics:

• Expectation Distance

  It is defined as $D_{Exp}=|\mathbb{E}[p_{eps}(r)]-\mathbb{E}[p(r)]|$, where $\mathbb{E}[p_{eps}(r)]$ and $\mathbb{E}[p(r)]$ are expectations of the output distributions with and without disturbance. After changing the first parameter, PSense genterates the symbolic expression for Expectation Distance as:

  ┌Analyzed parameter 1────────────┬
  │         │ Expectation Distance │ ...
  ├─────────┼──────────────────────┼───
  │ Bounds  │ Abs[eps]/(4          │ ...
  │         │ 8 + 12*eps)          │
  

  PSense finds the maximum value of the Expectation Distance with respect to the disturbance eps within $\pm 10\%$ of the original parameter

  ┌Analyzed parameter 1────────────┬
  │         │ Expectation Distance │ ...
  ├─────────┼──────────────────────┼───
  │ ...     │ ...                  │ ...
  │ Maximum │ 0.002032520          │ 
  │         │ 32520 eps            │ 
  │         │ -> 0.100000          │ 
  │         │ 000000 r1            │ 
  │         │ -> 0.999647          │ 
  │         │ 097614               │ 
  

  The result above shows the maximum value 0.00203 is obtained when eps $= -0.1$. PSense further analyzes whether the distance grows linearly when the disturbance |eps| increases:

  ┌Analyzed parameter 1────────────┬
  │         │ Expectation Distance │ ...
  ├─────────┼──────────────────────┼───
  │ ...     │ ...                  │ ...
  │ Linear  │ False                │
  └─────────┴──────────────────────┴
  

  In this example the Expectation Distance is not linear so PSense outputs False.

• Kolmogorov–Smirnov Statistic

  It is defined as $D_{KS}=\sup_{r\in support}|p_{eps}(r)-p(r)|$, where p_{eps}(r) and p(r) are the output cumulative density functions, and $\sup_{r\in support}$ represents the supremum of the distance over the support of $r$. PSense gives the distance $|p_{eps}(r)-p(r)|$ and the maximum value of $D_{KS}$, and then analyzes the linearity of $D_{KS}$.

  ┌Analyzed parameter 1───┬
  │         │ KS Distance │ ...
  ├─────────┼─────────────┼───
  │ Bounds  │ Abs[(eps*(- │ ...
  │         │ 1 + r1)*r1* │
  │         │ Boole[r1 != │
  │         │ 1])/(4 +    │
  │         │ eps)]/2     │
  │ Maximum │ 0.003048780 │ 
  │         │ 48780 eps   │ 
  │         │ -> 0.100000 │ 
  │         │ 000000 r1   │ 
  │         │ -> 0.499999 │ 
  │         │ 986837      │ 
  │ Linear  │ False       │
  └─────────┴─────────────┴
  

• Total Variation Distance

  It is defined as $D_{TVD}=\frac{1}{2}\int_{r\in support}|p_{eps}(r)-p(r)|$ for continuous distribution. PSense outputs the tightest linear upper and lower bound for the $D_{TVD}$ when the disturbance eps changes from 0 to 0.1:

  ┌Analyzed parameter 1───┬─
  │         │ TVD Bounds  │ 
  ├─────────┼─────────────┼─
  │ Bounds  │ -1.91842781 │ 
  │         │ 5330059*^-2 │ 
  │         │ 0 + 0.00138 │ 
  │         │ 23729270812 │ 
  │         │ 238*eps 0.0 │ 
  │         │ 00960929970 │ 
  │         │ 22092 + 0.0 │ 
  │         │ 01382372927 │ 
  │         │ 0812238*eps │ 
  │ Maximum │ 0.001016260 │ 
  │         │ 16260       │ 
  │         │ {eps -> 0.1 │ 
  │         │ 00000000000 │ 
  │         │             │ 
  │ Linear  │ NA          │ 
  └─────────┴─────────────┴─
  

• Kullback–Leibler Divergence

  It is defined as $D_{KL}=\int_{r\in support} p_{eps}(r) \log \frac{p_{eps}(r)}{p(r)}$ for continuous distribution. PSense outputs the tightest linear upper and lower bound for the $D_{TVD}$ when the disturbance eps changes from 0 to 0.1:

  ┌Analyzed parameter 1───┬─
  │         │ KL Bounds   │
  ├─────────┼─────────────┤
  │ Bounds  │ -8.65946098 │
  │         │ 6684*^-18 - │
  │         │ 0.029893770 │
  │         │ 465430913*e │
  │         │ ps 0.000071 │
  │         │ 15621843964 │
  │         │ 545 - 0.029 │
  │         │ 89377046543 │
  │         │ 0913*eps    │
  │ Maximum │ 0.002462657 │
  │         │ 85567       │
  │         │ {eps -> -0. │
  │         │ 08000000000 │
  │         │ 00          │
  │ Linear  │ NA          │
  └─────────┴─────────────┘
  

• See Tutorial 1 for metrics of discrete distributions.

User Specified Disturbance

You can set a value for the disturbance eps. Running the following to set eps to:

psense -f examples/unknown_vending_machine.psi -e 0.01

PSense would add 0.01 to each parameter in this program. It outputs the following:

Function Type:
Continuous
┌Analyzed parameter 1────────────┬─────────────┬─────────┬─────────┐
│         │ Expectation Distance │ KS Distance │ TVD     │ KL      │
├─────────┼──────────────────────┼─────────────┼─────────┼─────────┤
│ Maximum │ 1/4812               │ 0.00031     │ 0.00010 │ 0.00029 │
│         │                      │ 1720698     │ 3906899 │ 9884255 │
│         │                      │ 254 r1      │ 4181213 │ 3219106 │
│         │                      │ -> 0.50     │ 9       │ 3       │
│         │                      │ 0000000     │         │         │
│         │                      │ 000         │         │         │
└─────────┴──────────────────────┴─────────────┴─────────┴─────────┘
...

Notice now that eps becomes a concrete value, PSense directly outputs the numerical distances instead of a symbolic expression containing eps. For KS statistic, PSense further outputs which $r1$ value results in the maximum value.

Return to Tutorials